Complementaremos con los apuntes hasta la pagina 13.
También os dejo un ppt que en 5 minutos da una idea general del TEMA
PACO MATES nos explica muy bien este tema con sus videos de Pildoras Matemáticas.aqui
TEMA 2. MATRICES.
1. Tipos de Matrices.
1.1 Definición de matriz.
Una matriz es un conjunto ordenado en
una estructura de filas y columnas. Los elementos de
este conjunto pueden ser objetos matemáticos de muy variados tipos, aunque de
forma particular, trabajaremos exclusivamente con matrices formadas por números reales.Normalmente las
matrices son designadas por letras mayúsculas.
Los elementos
de una matriz se identifican por la fila y la columna que ocupan. Así,
designaremos por a32 el elemento que está situado en la tercera fila
y segunda columna de la matriz A.
El número de
filas y columnas que tiene una matriz se llama dimensión de
la matriz.
Dos matrices
son iguales si son de igual dimensión
y coincide el valor de los elementos que
ocupan la misma posición en ambas.
1.2 Tipos de matrices según su forma.
1.3 Tipos de matrices según sus elementos.
1.2 Matriz traspuesta.
2. Operaciones con matrices.
Este video esta muy instructivo
2.1 SUMA Y RESTA.
2.2 Producto número por matriz.
2.3 PRODUCTO MATRICES. Repasa los conceptos. Para multiplicar matriz A por matriz B tienen que suceder que A (m x n ) y B (n x p) . Es decir, numero de columnas de A coincidir con numero filas de B.
Veamos un video que agrupa estas operaciones:
2.4. PROPIEDADES
No conmutativas. No es lo mismo AxB que BxA ( en muchos casos es que alguno de ellas no se puede realizar)
No Simplifican. Quiere decir que AxB =AxC no da como conclusión B=C. No es verdad.
3. Potencias de Matrices
La potencia de una matriz no siempre se puede calcular. Sólo es posible cuando la matriz es cuadrada, es decir, cuando tiene el mismo número de filas que de columnas.
La peculiaridad de la potenciación de las matrices es que, en muchas matrices, las potencias siguen un patrón. Por ejemplo, las potencia -ésima de una matriz diagonal es también una matriz diagonal cuyos elementos de la diagonal son las potencias -ésimas de los elementos de la diagonal de la matriz :
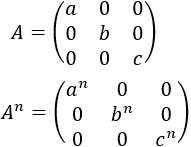
Por tanto, para muchas matrices, podemos encontrar una fórmula que nos proporcione la potencia -ésima sin la necesidad de calcular todas las potencias.
Para encontrar esta fórmula, tenemos que fijarnos en:
- La relación entre el exponente de la potencia y los elementos de la matriz. Por ejemplo, puede que algún elemento de la matriz sea el propio exponente.
- La paridad del exponente. Por ejemplo, puede ocurrir que las potencias pares sean de una forma y las impares de otra.
- Si hay distintos patrones. Por ejemplo, los exponentes múltiplos de un número pueden tener un patrón distinto a los que son múltiplos de otro.
- La variación de los signos. Por ejemplo, las potencias pares y las impares pueden cambiar de signos.
- Repetición. Por ejemplo, puede haya varias matrices que se repiten consecutivamente.
En definitiva, para obtener la fórmula tenemos que observar las primeras potencias y emplear nuestra intuición. Normalmente, con el cálculo de las primeras 3 ó 5 potencias, podremos deducir la fórmula. (MATRICES CÍCLICAS)
4. Aplicación de las matrices a la resolución de problemas.
4.1 Organización de datos.
4.2 Representación matricial de un sistema.
ver mas ejemplos en el siguiente enlace










