2º Bcto. Tema 4. Sistemas lineales con parámetros

4.1 Teorema de Rouché- Fröbenius. Gracias a www.hiru.eus 

Con el enunciado del teorema debido al francés Eugène Rouché y al alemán Georg Ferdinand Fröbenius se hace posible resolver cualquier tipo de sistema de ecuaciones de primer grado, tenga o no solución. En esencia, este teorema se basa en el análisis del rango de las matrices representativas del sistema.

Dado un sistema de m ecuaciones lineales con n incógnitas, cuya expresión general sería:

se pueden definir su matriz de coeficientes C y su matriz ampliada A como:

Según el teorema de Rouché-Fröbenius, la condición necesaria y suficiente para que un sistema de m ecuaciones lineales con n incógnitas sea compatible (tenga solución) es que el rango de la matriz de los coeficientes sea igual al rango de la matriz ampliada.

Discusión y clasificación de sistemas lineales

Como consecuencia de la aplicación del teorema de Rouché-Fröbenius, los sistemas de m ecuaciones lineales con n incógnitas se pueden discutir y resolver con cierta rapidez. Así, se tiene que:

• Si los rangos de las matrices de los coeficientes y ampliada son iguales, el sistema es compatible (tiene solución). Si el número de incógnitas es igual a dicho rango, será determinado (una solución), y si el número de incógnitas es mayor que el rango, el sistema es indeterminado (infinitas soluciones).
• Cuando los rangos de las matrices de los coeficientes y ampliada son distintos, el sistema es incompatible (no tiene solución).

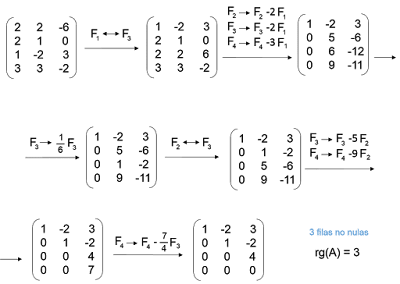
Discusión de un sistema por el teorema de Rouché-Fröbenius.

Resolución por el teorema de Rouché-Fröbenius

Para resolver un sistema de ecuaciones lineales basándose en el teorema de Rouché- Fröbenius, se procede del modo siguiente:

• Se discute el sistema, analizando los rangos de las matrices de coeficientes y ampliada.
• Si el sistema es compatible determinado, se toma el menor de la matriz de los coeficientes que ha dado el rango.
• El sistema equivalente que resulta se resuelve por la regla de Cramer .

   

4.2 Regla de Cramer y forma matricial.

Dado el sistema u₁x+v₁y+w₁z=b₁

                         u₂x+v₂y+w₂z=b₂

                         u₃x+v₃y+w₃z=b₃

4.3 Resolución de sistemas de cuatro ecuaciones.

Tutorial para la solución de sistemas de ecuaciones 4 incognitas de Jorge Villa

4.4 Discusión de un sistema con parámetros.

1. Hallamos el rango de la matriz de los coeficientes (rango C = r ).

2. Calculamos el rango de la matriz ampliada (rango A = r' ).

3. Aplicamos el teorema de Rouché.

·         r = r'               Sistema Compatible.

1. r = r'= n    Determinado.
2. r = r'≠ n    Indeterminado.

·         r ≠ r'               Sistema Incompatible.

4. Si el sistema es compatible determinado se resuelve por la regla de Cramer (se puede resolver mediante el método de Gauss que es mucho más fácil).

5. Si el sistema es compatible indeterminado se resuelve teniendo en cuenta que 

·         El número de ecuaciones = rango

·         El número de parámetros = nº de incógitas menos el rango

2 Bachillerato. Tema3 DETERMINANTES

Nos apoyamos en los siguientes apuntes

1. Determinantes de orden 2 y 3 por Sarrus.

1.1 ¿Qué es el determinante de una matriz?

1.2 Determinante de una matriz de orden 2 y 3 por Sarrus.

 

1.3 Casos en que el determinante es cero.

• Una línea es nula.
• Dos líneas paralelas son iguales.
• Dos líneas paralelas son proporcionales.
• Una línea es combinación lineal de otras paralelas a ellas.

línea puede ser COLUMNA O FILA.

2. Propiedades de los determinanes.

2.1 Cambiar líneas paralelas CAMBIA DE SIGNO..
2.2 Cambiar una línea por combinación lineal de otras NO CAMBIA DETERMINANTE.
2.3 Determinante de una matriz y su traspuesta ES EL MISMO.
2.4 Descomponer en suma. Los dos determinantes han de tener todas las lineas iguales a la original,menos una que es la suma.
2.5 Multiplicación por un número. Se multiplica solo una línea por dichonúmero.
2.6 Determinante del producto de dos matrices.Igual al producto de los determinantes.

3. Desarrollo de un determinante por los elementos de una línea.

3.1 Menor Complementario.

3.2 Adjunto.

3.3 Desarrollo práctico por adjuntos.

4. Matriz Inversa.
4.1 Matriz Adjunta.

4.2 Matriz Inversa.

4.3 Calculo de la Matriz Inversa.

 

Metodo Gauss-Jordan

4.4 REGLA DE ORO.No se puede calcular inversas cuando:

• La matriz no es cuadrada .
• Su determinante es 0.

5. Ecuaciones con matrices y determinantes.
5.1 Resolución de ecuaciones matriciales.

5.2 Resolución de ecuaciones con determinantes.

6. Rango de una matriz.
6.1 Calculo del RANGO por GAUSS.

vamos haciendo ceros mediante combinacion lineal de lineas hasta conseguir lo siguiente.

 

 

6.2 Calculo del rango matriz 3x3.

6.3 Vectores linealmente independientes o dependientes.
6.4 Discursion del rango de una matriz en función de un parametro.